Rankine Cycle

The Rankine cycle is a model that is used to predict the performance of steam turbine systems, though the theoretical principle also applies to reciprocating engines such as steam locomotives. The Rankine cycle is an idealized thermodynamic cycle of a heat engine that converts heat into mechanical work while undergoing phase change. The heat is supplied externally to a closed loop, which usually uses water as the working fluid. It is named after William John Macquorn Rankine, a Scottish polymath and Glasgow University professor.

Description

Physical layout of the four main devices used in the Rankine cycle

The Rankine cycle closely describes the process by which steam-operated heat engines commonly found in thermal power generation plants generate power.

Power depends on the temperature difference between a heat source and a cold source. The higher the difference, the more mechanical power can be efficiently extracted out of heat energy, as per Carnot’s theorem.

The heat sources used in these power plants are usually nuclear fission or the combustion of fossil fuels such as coal, natural gas, and oil. The higher the temperature, the better.

The efficiency of the Rankine cycle is limited by the high heat of vaporization of the working fluid. Also, unless the pressure and temperature reach super critical levels in the steam boiler, the temperature range the cycle can operate over is quite small: steam turbine entry temperatures are typically around 565 °C and steam condenser temperatures are around 30 °C. This gives a theoretical maximum Carnot efficiency for the steam turbine alone of about 63.8% compared with an actual overall thermal efficiency of up to 42% for a modern coal-fired power station. This low steam turbine entry temperature (compared to a gas turbine) is why the Rankine (steam) cycle is often used as a bottoming cycle to recover otherwise rejected heat in combined-cycle gas turbine power stations.

The cold source (the colder the better) used in these power plants are usually cooling towers and a large water body (river or sea). The efficiency of the Rankine cycle is limited on the cold side by the lower practical temperature of the working fluid.

The working fluid in a Rankine cycle follows a closed loop and is reused constantly. The water vapor with condensed droplets often seen billowing from power stations is created by the cooling systems (not directly from the closed-loop Rankine power cycle). This ‘exhaust’ heat is represented by the “Qout” flowing out of the lower side of the cycle shown in the T/s diagram below. Cooling towers operate as large heat exchangers by absorbing the latent heat of vaporization of the working fluid and simultaneously evaporating cooling water to the atmosphere.

While many substances could be used as the working fluid in the Rankine cycle, water is usually the fluid of choice due to its favorable properties, such as its non-toxic and unreactive chemistry, abundance, and low cost, as well as its thermodynamic properties. By condensing the working steam vapor to a liquid the pressure at the turbine outlet is lowered and the energy required by the feed pump consumes only 1% to 3% of the turbine output power and these factors contribute to a higher efficiency for the cycle. The benefit of this is offset by the low temperatures of steam admitted to the turbine(s). Gas turbines, for instance, have turbine entry temperatures approaching 1500°C. However, the thermal efficiency of actual large steam power stations and large modern gas turbine stations are similar.

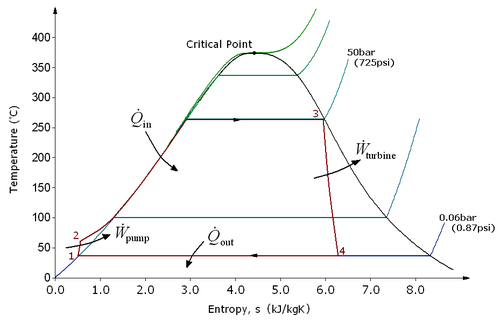
The four processes in the Rankine cycle

T-s diagram of a typical Rankine cycle operating between pressures of 0.06bar and 50bar. Left of the bell shaped curve there is liquid, right of it there is gas and under it there is saturated liquid-vapour equilibrium.

There are four processes in the Rankine cycle. These states are identified by numbers (in brown) in the above T-s diagram.

  • Process 1-2: The working fluid is pumped from low to high pressure. As the fluid is a liquid at this stage, the pump requires little input energy.
  • Process 2-3: The high pressure liquid enters a boiler where it is heated at constant pressure by an external heat source to become a dry saturated vapour. The input energy required can be easily calculated graphically, using an enthalpy-entropy chart (aka h-s chart or Mollier diagram), or numerically, using steam tables.
  • Process 3-4: The dry saturated vapour expands through a turbine, generating power. This decreases the temperature and pressure of the vapour, and some condensation may occur. The output in this process can be easily calculated using the chart or tables noted above.
  • Process 4-1: The wet vapour then enters a condenser where it is condensed at a constant pressure to become a saturated liquid.

In an ideal Rankine cycle the pump and turbine would be isentropic, i.e., the pump and turbine would generate no entropy and hence maximize the net work output. Processes 1-2 and 3-4 would be represented by vertical lines on the T-s diagram and more closely resemble that of the Carnot cycle. The Rankine cycle shown here prevents the vapor ending up in the superheat region after the expansion in the turbine, [1] which reduces the energy removed by the condensers.

The actual vapor power cycle differs from the ideal Rankine cycle because of irreversibilities in the inherent components caused by fluid friction and heat loss to the surroundings; fluid friction causes pressure drops in the boiler, the condenser, and the piping between the components, and as a result the steam leaves the boiler at a lower pressure; heat loss reduces the net work output, thus heat addition to the steam in the boiler is required to maintain the same level of net work output.

Variables

Q ˙ {\displaystyle {\dot {Q}}} {\dot {Q}} Heat flow rate to or from the system (energy per unit time)
m ˙ {\displaystyle {\dot {m}}} {\dot {m}} Mass flow rate (mass per unit time)
W ˙ {\displaystyle {\dot {W}}} \dot{W} Mechanical power consumed by or provided to the system (energy per unit time)
η t h e r m {\displaystyle \eta _{therm}} \eta_{therm} Thermodynamic efficiency of the process (net power output per heat input, dimensionless)
η p u m p , η t u r b {\displaystyle \eta _{pump},\eta _{turb}} \eta_{pump},\eta_{turb} Isentropic efficiency of the compression (feed pump) and expansion (turbine) processes, dimensionless
h 1 , h 2 , h 3 , h 4 {\displaystyle h_{1},h_{2},h_{3},h_{4}} h_1, h_2, h_3, h_4 The “specific enthalpies” at indicated points on the T-S diagram
h 4 s {\displaystyle h_{4s}} h_{4s} The final “specific enthalpy” of the fluid if the turbine were isentropic
p 1 , p 2 {\displaystyle p_{1},p_{2}} p_1, p_2 The pressures before and after the compression process

Equations

In general, the efficiency of a simple rankine cycle can be written as:

η t h e r m = W ˙ t h e r m a l − W ˙ Q ˙ i n ≈ W ˙ t u r b Q ˙ i n . {\displaystyle \eta _{therm}={\frac {{\dot {W}}_{thermal}-{\dot {W}}_{}}{{\dot {Q}}_{in}}}\approx {\frac {{\dot {W}}_{turb}}{{\dot {Q}}_{in}}}.} \eta _{{therm}}={\frac {{\dot {W}}_{{thermal}}-{\dot {W}}_{{}}}{{\dot {Q}}_{{in}}}}\approx {\frac {{\dot {W}}_{{turb}}}{{\dot {Q}}_{{in}}}}.

Each of the next four equations[1] is derived from the energy and mass balance for a control volume. η t h e r m {\displaystyle \eta _{therm}} \eta_{therm} defines the thermodynamic efficiency of the cycle as the ratio of net power output to heat input. As the work required by the pump is often around 1% of the turbine work output, it can be simplified.

Q ˙ i n m ˙ = h 3 − h 2 {\displaystyle {\frac {{\dot {Q}}_{in}}{\dot {m}}}=h_{3}-h_{2}} \frac{\dot{Q}_{in}}{\dot{m}}=h_3-h_2
Q ˙ o u t m ˙ = h 4 − h 1 {\displaystyle {\frac {{\dot {Q}}_{out}}{\dot {m}}}=h_{4}-h_{1}} \frac{\dot{Q}_{out}}{\dot{m}}=h_4-h_1
W ˙ p u m p m ˙ = h 2 − h 1 {\displaystyle {\frac {{\dot {W}}_{pump}}{\dot {m}}}=h_{2}-h_{1}} \frac{\dot{W}_{pump}}{\dot{m}}=h_2-h_1
W ˙ t u r b i n e m ˙ = h 3 − h 4 {\displaystyle {\frac {{\dot {W}}_{turbine}}{\dot {m}}}=h_{3}-h_{4}} \frac{\dot{W}_{turbine}}{\dot{m}}=h_3-h_4

When dealing with the efficiencies of the turbines and pumps, an adjustment to the work terms must be made.

W ˙ p u m p m ˙ = h 2 − h 1 ≈ v 1 Δ p η p u m p = v 1 ( p 2 − p 1 ) η p u m p {\displaystyle {\frac {{\dot {W}}_{pump}}{\dot {m}}}=h_{2}-h_{1}\approx {\frac {v_{1}\Delta p}{\eta _{pump}}}={\frac {v_{1}(p_{2}-p_{1})}{\eta _{pump}}}} \frac{\dot{W}_{pump}}{\dot{m}} = h_2 - h_1 \approx \frac{v_1 \Delta p}{\eta_{pump}} = \frac{v_1 ( p_2 - p_1 )}{\eta_{pump}}
W ˙ t u r b i n e m ˙ = h 3 − h 4 ≈ ( h 3 − h 4 ) η t u r b i n e {\displaystyle {\frac {{\dot {W}}_{turbine}}{\dot {m}}}=h_{3}-h_{4}\approx (h_{3}-h_{4})\eta _{turbine}} \frac{\dot{W}_{turbine}}{\dot{m}} = h_3-h_4 \approx (h_3-h_4) \eta_{turbine}

Real Rankine cycle (non-ideal)

Rankine cycle with superheat

In a real power plant cycle (the name ‘Rankine’ cycle is used only for the ideal cycle), the compression by the pump and the expansion in the turbine are not isentropic. In other words, these processes are non-reversible and entropy is increased during the two processes. This somewhat increases the power required by the pump and decreases the power generated by the turbine.

In particular the efficiency of the steam turbine will be limited by water droplet formation. As the water condenses, water droplets hit the turbine blades at high speed causing pitting and erosion, gradually decreasing the life of turbine blades and efficiency of the turbine. The easiest way to overcome this problem is by superheating the steam. On the Ts diagram above, state 3 is at a border of the two phase region of steam and water so after expansion the steam will be very wet. By superheating, state 3 will move to the right (and up) in the diagram and hence produce a drier steam after expansion.

Variations of the basic Rankine cycle

The overall thermodynamic efficiency can be increased by raising the average heat input temperature ( T ¯ i n = ∫ 2 3 T d Q Q i n ) {\displaystyle \left({\bar {T}}_{\mathit {in}}={\frac {\int _{2}^{3}T\,dQ}{Q_{\mathit {in}}}}\right)} \left({\bar {T}}_{{\mathit {in}}}={\frac {\int _{2}^{3}T\,dQ}{Q_{{\mathit {in}}}}}\right) of that cycle. Increasing the temperature of the steam into the superheat region is a simple way of doing this. There are also variations of the basic Rankine cycle which are designed to raise the thermal efficiency of the cycle in this way; two of these are described below.

Rankine cycle with reheat

Rankine cycle with reheat

The purpose of a reheating cycle is to remove the moisture carried by the steam at the final stages of the expansion process. In this variation, two turbines work in series. The first accepts vapor from the boiler at high pressure. After the vapor has passed through the first turbine, it re-enters the boiler and is reheated before passing through a second, lower-pressure, turbine. The reheat temperatures are very close or equal to the inlet temperatures, whereas the optimum reheat pressure needed is only one fourth of the original boiler pressure. Among other advantages, this prevents the vapor from condensing during its expansion and thereby damaging the turbine blades, and improves the efficiency of the cycle, because more of the heat flow into the cycle occurs at higher temperature. The reheat cycle was first introduced in the 1920s, but was not operational for long due to technical difficulties. In the 1940s, it was reintroduced with the increasing manufacture of high-pressure boilers, and eventually double reheating was introduced in the 1950s. The idea behind double reheating is to increase the average temperature. It was observed that more than two stages of reheating are unnecessary, since the next stage increases the cycle efficiency only half as much as the preceding stage. Today, double reheating is commonly used in power plants that operate under supercritical pressure.

Regenerative Rankine cycle

Regenerative Rankine cycle

The regenerative Rankine cycle is so named because after emerging from the condenser (possibly as a subcooled liquid) the working fluid is heated by steam tapped from the hot portion of the cycle. On the diagram shown, the fluid at 2 is mixed with the fluid at 4 (both at the same pressure) to end up with the saturated liquid at 7. This is called “direct contact heating”. The Regenerative Rankine cycle (with minor variants) is commonly used in real power station.

Another variation sends bleed steam from between turbine stages to feedwater heaters to preheat the water on its way from the condenser to the boiler. These heaters do not mix the input steam and condensate, function as an ordinary tubular heat exchanger, and are named “closed feedwater heaters”.

Regeneration increases the cycle heat input temperature by eliminating the addition of heat from the boiler/fuel source at the relatively low feedwater temperatures that would exist without regenerative feedwater heating. This improves the efficiency of the cycle, as more of the heat flow into the cycle occurs at higher temperature.

Organic Rankine cycle

Main article: Organic Rankine cycle

The organic Rankine cycle (ORC) uses an organic fluid such as n-pentane[1] or toluene[2] in place of water and steam. This allows use of lower-temperature heat sources, such as solar ponds, which typically operate at around 70–90 °C.[3] The efficiency of the cycle is much lower as a result of the lower temperature range, but this can be worthwhile because of the lower cost involved in gathering heat at this lower temperature. Alternatively, fluids can be used that have boiling points above water, and this may have thermodynamic benefits. See, for example, mercury vapour turbine.

The Rankine cycle does not restrict the working fluid in its definition, so the name “organic cycle” is simply a marketing concept and the cycle should not be regarded as a separate thermodynamic cycle.

Supercritical Rankine cycle

The Rankine cycle applied using a supercritical fluid[4] combines the concepts of heat regeneration and supercritical Rankine cycle into a unified process called the Regenerative Supercritical Cycle (RGSC) cycle. It is optimised for temperature sources 125 – 450°C.

References

Wikimedia Commons has media related to Rankine cycle.

 

Moghtaderi, Behdad (2009). “An Overview of GRANEX Technology for Geothermal Power Generation and Waste Heat Recovery”. Australian Geothermal Energy Conference 2009. , Inc.